Understanding Ark Liquidity Requirements

This post discusses the liquidity requirements and calculates the funding needs of Ark Service Provider (ASP), as all transactions within Ark must be funded by the ASP.
What is Ark?
Ark is a promising second-layer solution for Bitcoin that improves the scalability and privacy of the network. It offers the following benefits:
- No incoming liquidity required: Receivers can accept payments without having to worry about having enough funds in their wallets.
- Confidential payments: Ark protects the confidentiality of recipients, which is not always possible with other second-layer solutions.
- Scalable: Ark is a solution for enabling the scalability of Bitcoin and applications and services which utilize the Bitcoin infrastructure.
- Secure: Ark is a secure solution that is built on top of the Bitcoin blockchain.
Ark liquidity requirements
Introduction
When Alice wishes to board an Ark, she finances an output that is eligible to be recognized as a VTXO in a future round. This does not necessitate any liquidity from the ASP:
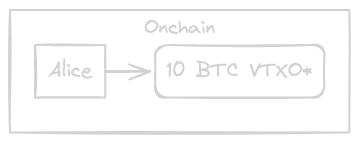
When Alice makes her initial payment, for example, 1 BTC to Bob, the VTXO* will be utilized to finance the Round transaction, so again, the ASP will not need to supply any additional liquidity. But if Alice tries to make a second payment, for example, 1 BTC to Charlie, she will now be utilizing a genuine virtual VTXO. In this case, the ASP will need to finance the following Round transaction:
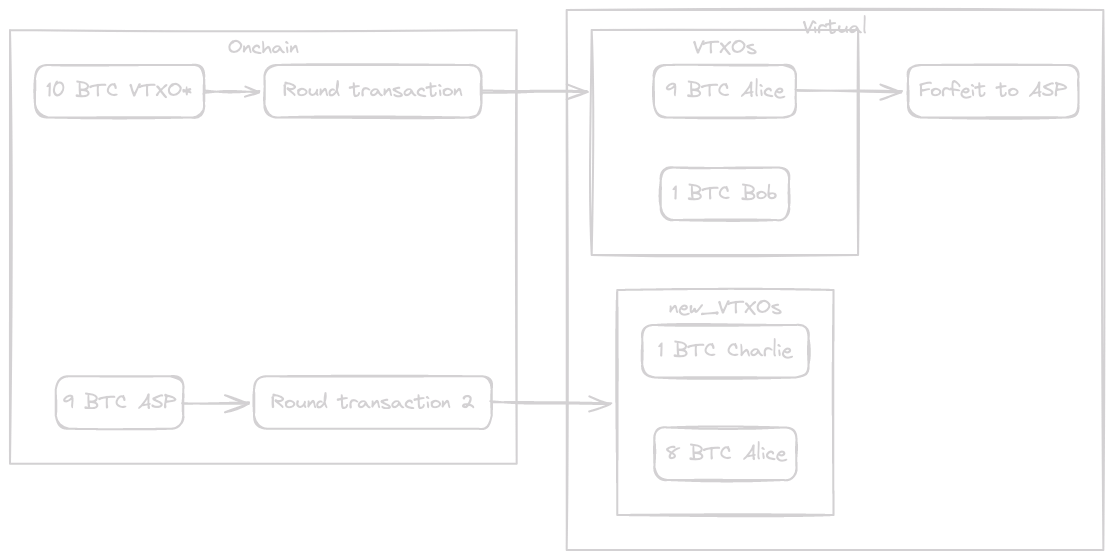
Finally, let's assume Alice also pays 1 BTC to Dave:
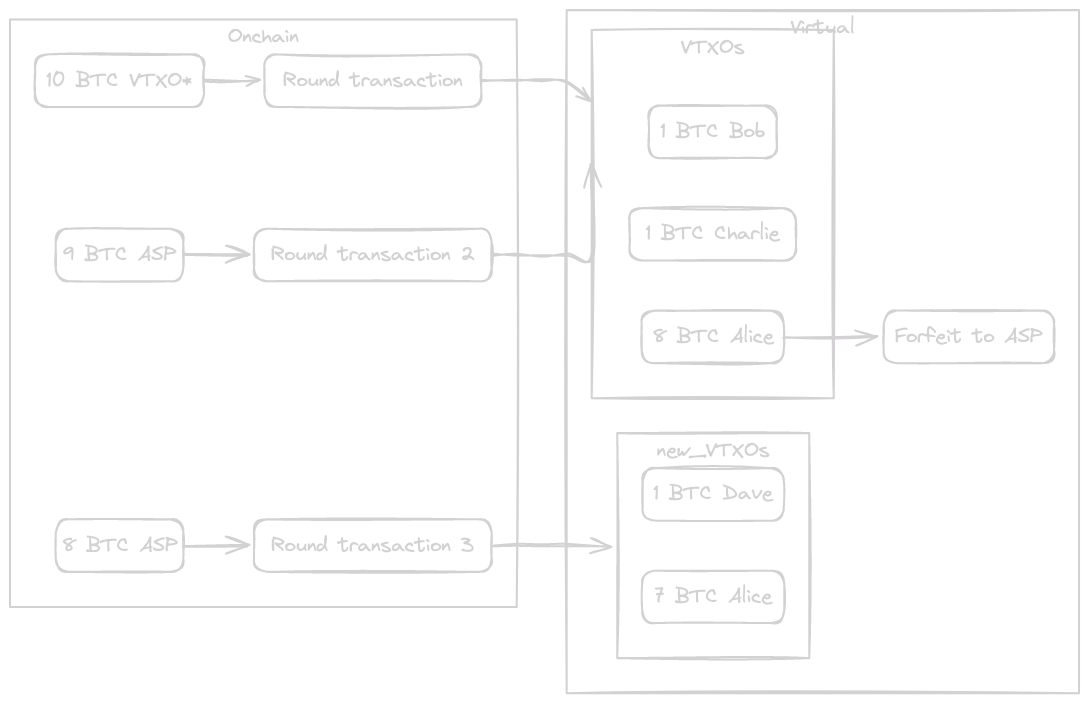
Summary
- 10 BTC initial onboard from Alice
- 4 payments:
- Alice => Bob 1 BTC
- Alice => Charlie 1 BTC
- Alice => Dave 1 BTC
- total payments = 3 BTC
- ASP liquidity needed = 17 BTC
As we can see, the liquidity needs for the ASP depends on the following factors:
- Capital onboarded
- Value of the payments
The liquidity problem
If the ASP exhausts its liquidity, it will have to cease accepting new payments and will be compelled to wait for the timelocks (4 weeks) on the on-chain transactions to expire in order to regain liquidity.
To avoid the ASP from running out of funds, it must be able to anticipate how much liquidity will be required throughout a 4 week period.
As we observed, the liquidity necessary during a period will rely on the capital onboarded and the number and value of payments made with that capital
Given this, we can assume the liquidity needed will be the consequence of a function of capital onboarded and a percentage of this capital utilized during the 4 weeks period.
Therefore, how much capital can an ASP accept from users without risking not having enough capital to finance payments inside Ark? In other words, what proportion of the capital inside an Ark is transferred in a 4 week period?
This is similar to the definition of Money Velocity, as defined by the St. Louis Fed:
The velocity of money is the frequency at which one unit of currency is used to purchase domestically-produced goods and services within a given time period.
Money Velocity (MV)
Here are some Money Velocity numbers:
- USD (Q3 2023): 1.327
- Lightning (August 2023): 0.59 per month
If we use a Money Velocity of 1.00 (for simplicity), this means that each BTC inside the Ark will be spent once (1.00) during that given period. Since the ASP must fund all transactions and onboarding, this means that for each 1 BTC added to the Ark, the ASP will need 1 BTC to fund the onboarding and 1 BTC to fund the transfers inside the Ark. With an initial balance of 100 BTC, this results in a limit of 50 BTC allowed to onboard (100 = 50 for onboarding + 50 for trades).
If MV = 0.59, this means that those initial 100 BTC would allow for 62.89 BTC of onboarding, where (100 = 62.89 for onboarding + (69.89 * 0.59 = 37.11) for trades).
In reality, the Money Velocity of Ark is likely to be somewhere between 1.00 and 0.59. This means that the ASP will need to have a certain amount of liquidity on hand to fund both onboarded BTC and transfers inside the Ark. The amount of liquidity required will depend on the specific Money Velocity of Ark, which is not yet known for sure.
Comparison table:
| Money Velocity | Balance | +Onboard (BTC) | Inside Ark (BTC) | Transfers (BTC) |
|---|---|---|---|---|
| 0.59 | 100.00 | 62.89 | 0.00 | 37.11 |
| 1.00 | 100.00 | 50.00 | 0.00 | 50.00 |
| 1.327 | 100.00 | 42.97 | 0.00 | 57.03 |
After one month, all the funds used by the ASP, plus the funds sent by the users, become available again. This means that the ASP will have more available liquidity, so it can increase the allowed value for onboards. On the other hand, there is now more capital inside the Ark, so the ASP needs to reserve more capital to fund the transfers:
| Money Velocity | Balance | +Onboard (BTC) | Inside Ark (BTC) | Transfers (BTC) |
|---|---|---|---|---|
| 0.59 | 162.89 | 79.11 | 62.89 | 83.78 |
| 1.00 | 150 | 50.00 | 50.00 | 100.00 |
| 1.327 | 142.97 | 36.93 | 42.97 | 57.03 |
Now, what would happen in a one-year period?
info
You can run your own simulations with the Ark liquidity simulator.
Simulating for 1 year
Columns definition:
- Inside Ark = Accumulated of allowed onboards
- ASP Balance = Initial balance + Inside Ark
- Reserved for trades = Inside Ark * MV
- Remaining = Balance - Reserved for trades
- Allowed onboards = Remaining / (1 + MV)
Money Velocity: 0.59
| Month | Inside Ark | ASP Balance | Reserved for trades | Remaining | Allowed onboards |
|---|---|---|---|---|---|
| 0 | 0.00 | 100.00 | 0.00 | 100.00 | 0.00 |
| 1 | 0.00 | 100.00 | 0.00 | 100.00 | 62.89 |
| 2 | 62.89 | 162.89 | 37.11 | 125.79 | 79.11 |
| 3 | 142.00 | 242.00 | 83.78 | 158.22 | 99.51 |
| 4 | 241.51 | 341.51 | 142.49 | 199.02 | 125.17 |
| 5 | 366.68 | 466.68 | 216.34 | 250.34 | 157.45 |
| 6 | 524.13 | 624.13 | 309.24 | 314.89 | 198.05 |
| 7 | 722.18 | 822.18 | 426.09 | 396.09 | 249.12 |
| 8 | 971.29 | 1,071.29 | 573.06 | 498.23 | 313.35 |
| 9 | 1,284.65 | 1,384.65 | 757.94 | 626.70 | 394.15 |
| 10 | 1,678.80 | 1,778.80 | 990.49 | 788.31 | 495.79 |
| 11 | 2,174.59 | 2,274.59 | 1,283.01 | 991.58 | 623.64 |
| 12 | 2,798.23 | 2,898.23 | 1,650.95 | 1,247.27 | 784.45 |
Money Velocity: 1
| Month | Inside Ark | ASP Balance | Reserved for trades | Remaining | Allowed onboards |
|---|---|---|---|---|---|
| 0 | 0.00 | 100.00 | 0.00 | 100.00 | 0.00 |
| 1 | 0.00 | 100.00 | 0.00 | 100.00 | 50.00 |
| 2 | 50.00 | 150.00 | 50.00 | 100.00 | 50.00 |
| 3 | 100.00 | 200.00 | 100.00 | 100.00 | 50.00 |
| 4 | 150.00 | 250.00 | 150.00 | 100.00 | 50.00 |
| 5 | 200.00 | 300.00 | 200.00 | 100.00 | 50.00 |
| 6 | 250.00 | 350.00 | 250.00 | 100.00 | 50.00 |
| 7 | 300.00 | 400.00 | 300.00 | 100.00 | 50.00 |
| 8 | 350.00 | 450.00 | 350.00 | 100.00 | 50.00 |
| 9 | 400.00 | 500.00 | 400.00 | 100.00 | 50.00 |
| 10 | 450.00 | 550.00 | 450.00 | 100.00 | 50.00 |
| 11 | 500.00 | 600.00 | 500.00 | 100.00 | 50.00 |
| 12 | 550.00 | 650.00 | 550.00 | 100.00 | 50.00 |
Money Velocity 1.327
| Month | Inside Ark | ASP Balance | Reserved for trades | Remaining | Allowed onboards |
|---|---|---|---|---|---|
| 0 | 0.00 | 100.00 | 0.00 | 100.00 | 0.00 |
| 1 | 0.00 | 100.00 | 0.00 | 100.00 | 42.97 |
| 2 | 42.97 | 142.97 | 57.03 | 85.95 | 36.93 |
| 3 | 79.91 | 179.91 | 106.04 | 73.87 | 31.74 |
| 4 | 111.65 | 211.65 | 148.16 | 63.49 | 27.28 |
| 5 | 138.94 | 238.94 | 184.37 | 54.57 | 23.45 |
| 6 | 162.39 | 262.39 | 215.49 | 46.90 | 20.15 |
| 7 | 182.54 | 282.54 | 242.23 | 40.31 | 17.32 |
| 8 | 199.86 | 299.86 | 265.22 | 34.64 | 14.89 |
| 9 | 214.75 | 314.75 | 284.98 | 29.78 | 12.80 |
| 10 | 227.55 | 327.55 | 301.96 | 25.59 | 11.00 |
| 11 | 238.55 | 338.55 | 316.55 | 22.00 | 9.45 |
| 12 | 248.00 | 348.00 | 329.09 | 18.90 | 8.12 |
Results
Simulating the three different MV values over a one-year period, we can conclude the following:
- If MV < 1, the ASP can onboard more BTC each month than in the previous month.
- If MV = 1, the allowed value for onboarding BTC is always the same (half of the initial balance).
- If MV > 1, the value of allowed BTC to onboard converges to 0 over time, with the maximum onboard value equal to (initial balance) / (MV - 1).
The Money Velocity (MV) for USD is quarterly. Assuming that M2 is constant and GDP is evenly distributed over the three months, the MV for one month should be ⅓ of the MV for the quarter, or 0.33.
Algorithm
Allowed onboard value
The value of allowed onboard BTC for this round will be:
Allowed onboard formula
(Available balance - User’s funds in Ark * MV) / (1 + MV)
Where:
- Available balance = Initial ASP balance + User’s funds
- User’s funds = All BTC onboarded by users until now
- MV = Money Velocity
Money Velocity
To calculate the value of Money Velocity:
Money Velocity formula
Average for the last N rounds of (amount transferred / user’s funds)
Rational
The ASP keeps records of onboarded and transferred amounts from previous rounds, and uses them to calculate the Money Velocity (MV) for the current round. It then uses the MV to calculate the maximum amount that can be onboarded in the current round.
If you've read this far, thank you! But now it's time for the bad news.
The UTXO model
How the UTXO Model Works
The change problem
But since Ark uses a UTXO model, this MV theory doesn't work, as the ASP will also need to fund the change on each transaction. For example, if Alice has a 1 BTC VTXO and wants to pay Bob 0.2 BTC, the ASP will need to fund two new VTXOs:
- 0.2 BTC to Bob
- 0.8 BTC to Alice (change)
Some simulations
Imagine that Alice boarded the Ark with 1 BTC. She has a 1 BTC VTXO and spends ⅓ of her money in the first month (MV = 0.33) using three payments of 0.11 BTC each.
Let's also assume that these payments are inside Ark (to Bob), which means that the ASP will also need to fund Bob's VTXO.
| Payment | Value | Alice VTXO | Bob VTXOs (0.11 each) | Liquidity needed | Liquidity accum |
|---|---|---|---|---|---|
| 0 | 0 | 1.00 | 0 | 0 | 0 |
| 1 | 0.11 | 0.89 | 1 | 1.00 | 1.00 |
| 2 | 0.11 | 0.78 | 2 | 0.89 | 1.89 |
| 3 | 0.11 | 0.67 | 3 | 0.78 | 2.67 |
At the end of the transaction, Alice has one VTXO of 0.67 BTC and Bob has three VTXOs of 0.11 BTC each.
Huge funding needs (factor of 8)
The ASP needed 2.67 of liquidity to support 0.33 traded inside Ark.
Things get much worse if the user makes 10 payments instead of 3 (spending 0.033 BTC on each):
| Payment | Value | Alice VTXO | Bob VTXOs (0.033 each) | Liquidity needed | Liquidity accum |
|---|---|---|---|---|---|
| 0 | 0 | 1.00 | 0 | 0 | 0 |
| 1 | 0.033 | 0.97 | 1 | 1.00 | 1.00 |
| 2 | 0.033 | 0.93 | 2 | 0.97 | 1.97 |
| 3 | 0.033 | 0.90 | 3 | 0.93 | 2.90 |
| 4 | 0.033 | 0.87 | 4 | 0.90 | 3.80 |
| 5 | 0.033 | 0.84 | 5 | 0.87 | 4.67 |
| 6 | 0.033 | 0.80 | 6 | 0.84 | 5.51 |
| 7 | 0.033 | 0.77 | 7 | 0.80 | 6.31 |
| 8 | 0.033 | 0.74 | 8 | 0.77 | 7.08 |
| 9 | 0.033 | 0.70 | 9 | 0.74 | 7.81 |
| 10 | 0.033 | 0.67 | 10 | 0.70 | 8.52 |
Huge funding needs (factor of 25)
The ASP needed 8.52 of liquidity to support 0.33 traded inside Ark.
Possible mitigations
One can try to reduce these liquidity requirements by pushing several levers:
- Reduce MV by reducing the timelock (e.g., 2 weeks instead of 1 month).
- Reduce transaction change by creating a set of UTXOs with a range of values on the first place, and then doing coin selection with the purpose of reducing change to the minimum possible.
Reduce transaction change
- Assuming MV = 0.33, and 10 payments of equal value during a month period
- Dividing Alice’s initial UTXO into 10, 100, and 1000 VTXOs
Using a 1:10 ratio for VTXOs:
| VTXO Value | Payment number | Payment value | VTXOs used | Alice balance | Alice VTXOs | Liquidity needed | Liquidity accum |
|---|---|---|---|---|---|---|---|
| 0.1 | 0 | 0.000 | 0 | 1.000 | 10 | 0.0 | 0.00 |
| 0.1 | 1 | 0.033 | 1 | 0.967 | 10 | 0.1 | 0.10 |
| 0.1 | 2 | 0.033 | 1 | 0.934 | 10 | 0.1 | 0.20 |
| 0.1 | 3 | 0.033 | 1 | 0.901 | 10 | 0.1 | 0.30 |
| 0.1 | 4 | 0.033 | 1 | 0.868 | 10 | 0.1 | 0.40 |
| 0.1 | 5 | 0.033 | 1 | 0.835 | 10 | 0.1 | 0.50 |
| 0.1 | 6 | 0.033 | 1 | 0.802 | 10 | 0.1 | 0.60 |
| 0.1 | 7 | 0.033 | 1 | 0.769 | 10 | 0.1 | 0.70 |
| 0.1 | 8 | 0.033 | 1 | 0.736 | 10 | 0.1 | 0.80 |
| 0.1 | 9 | 0.033 | 1 | 0.703 | 10 | 0.1 | 0.90 |
| 0.1 | 10 | 0.033 | 1 | 0.670 | 10 | 0.1 | 1.00 |
Using a 1:100 ratio for VTXOs:
| VTXO Value | Payment number | Payment value | VTXOs used | Alice balance | Alice VTXOs | Liquidity needed | Liquidity accum |
|---|---|---|---|---|---|---|---|
| 0.01 | 0 | 0.000 | 0 | 1.000 | 100 | 0.0 | 0.00 |
| 0.01 | 1 | 0.033 | 4 | 0.967 | 97 | 0.04 | 0.04 |
| 0.01 | 2 | 0.033 | 4 | 0.934 | 94 | 0.04 | 0.08 |
| 0.01 | 3 | 0.033 | 4 | 0.901 | 91 | 0.04 | 0.12 |
| 0.01 | 4 | 0.033 | 4 | 0.868 | 88 | 0.04 | 0.16 |
| 0.01 | 5 | 0.033 | 4 | 0.835 | 85 | 0.04 | 0.20 |
| 0.01 | 6 | 0.033 | 4 | 0.802 | 82 | 0.04 | 0.24 |
| 0.01 | 7 | 0.033 | 4 | 0.769 | 79 | 0.04 | 0.28 |
| 0.01 | 8 | 0.033 | 4 | 0.736 | 76 | 0.04 | 0.32 |
| 0.01 | 9 | 0.033 | 4 | 0.703 | 73 | 0.04 | 0.36 |
| 0.01 | 10 | 0.033 | 4 | 0.670 | 70 | 0.04 | 0.40 |
Using a 1:1000 ratio for VTXOs:
| VTXO Value | Payment number | Payment value | VTXOs used | Alice balance | Alice VTXOs | Liquidity needed | Liquidity accum |
|---|---|---|---|---|---|---|---|
| 0.001 | 0 | 0.000 | 0 | 1.000 | 1000 | 0.0 | 0.00 |
| 0.001 | 1 | 0.033 | 33 | 0.967 | 968 | 0.033 | 0.03 |
| 0.001 | 2 | 0.033 | 33 | 0.934 | 936 | 0.033 | 0.07 |
| 0.001 | 3 | 0.033 | 33 | 0.901 | 904 | 0.033 | 0.10 |
| 0.001 | 4 | 0.033 | 33 | 0.868 | 872 | 0.033 | 0.13 |
| 0.001 | 5 | 0.033 | 33 | 0.835 | 840 | 0.033 | 0.17 |
| 0.001 | 6 | 0.033 | 33 | 0.802 | 808 | 0.033 | 0.20 |
| 0.001 | 7 | 0.033 | 33 | 0.769 | 776 | 0.033 | 0.23 |
| 0.001 | 8 | 0.033 | 33 | 0.736 | 744 | 0.033 | 0.26 |
| 0.001 | 9 | 0.033 | 33 | 0.703 | 712 | 0.033 | 0.30 |
| 0.001 | 10 | 0.033 | 33 | 0.670 | 680 | 0.033 | 0.33 |
Comparison table:
| VTXO ratio | MV | # Payments | ASP liquidity needed |
|---|---|---|---|
| 10 | 0.33 | 10 | 1.00 |
| 100 | 0.33 | 10 | 0.40 |
| 1000 | 0.33 | 10 | 0.33 |
conclusion
Dividing the initial UTXO into more VTXOs decreases the need for funding.
Conclusion
The liquidity requirements for an ASP will depend on three major factors:
- Money Velocity: This is not under the control of the ASP, and if it is higher than 1, the Ark capacity will converge to a fixed value.
- The locktime period on VTXOs: Reducing the locktime period will return the locked liquidity sooner. However, this also means that users will need to "recycle" their VTXOs sooner, which can be seen as a worse user experience.
- The VTXO ratio: In other words, this is the maximum allowed value for a given VTXO. At one extreme, the ASP could force all VTXOs to be of 1 sat, which would eliminate any "wasted" liquidity on change. However, this would also require millions of signatures from the user and ASP to construct a payment, which would cause a worse user experience.
